En el mundo de la Seguridad de la Información, gestionar los riesgos no es una opción, es una necesidad. Para navegar en este entorno complejo, necesitamos herramientas que nos ofrezcan una visión clara y cuantificable a través del uso de una metodología sistemática y repetible. Una de las más reconocidas en el ámbito de habla hispana es PILAR.
Pero, ¿alguna vez te has preguntado qué hay detrás de sus informes? ¿Cómo llega PILAR a la conclusión de que un riesgo es de 6,8 en lugar de 4,2? Vamos a desgranar su motor interno e intentar explicar, de una manera sencilla, el algoritmo que utiliza para calcular el riesgo.
PILAR es una herramienta que ayuda a analizar y gestionar los riesgos en sistemas de información. Utiliza la metodología Magerit, y ha sido desarrollada con el apoyo del Centro Criptológico Nacional (CCN). Se actualiza regularmente y existen diferentes versiones.
Se puede encontrar documentación relativa al uso de la misma en los canales oficiales.
La Lógica del Riesgo: Un Proceso en 6 Pasos.
A través de estos pasos vamos a intentar con un ejemplo lo más simple posible cómo funciona el algoritmo de PILAR.
Paso 1: Valorar los Activos
Todo análisis de riesgos comienza por identificar y valorar lo que queremos proteger: nuestros activos. Un activo no es solo un servidor o un ordenador; puede ser la base de datos de clientes, la reputación de la marca o la continuidad de un servicio crítico. Estos se valoran en PILAR en distintas dimensiones. Para simplificar consideraremos sólo una de ellas la Integridad y al activo de ejemplo le asignaremos un valor de 10 en dicha dimensión.
Paso 2: Identificar Amenazas
Una vez que conocemos el valor de nuestros activos, identificamos los peligros que les acechan: las amenazas. Para cada par «activo-amenaza», PILAR nos pide analizar dos cosas:
- Degradación: El daño potencial que la amenaza causaría en cada una de las cinco dimensiones, expresado en un porcentaje (de 0% a 100%).
- Probabilidad: La probabilidad de que esa amenaza se materialice. PILAR generalmente usa una escala de 1 a 5 aunque se pueden usar valores ARO (Annual Rate of Occurrence, frecuencia esperada de ocurrencia). PILAR puede asumir valores automáticos consensuados por la industria.
Ejemplo Amenaza
Degradación en la dimensión Integridad del 100%
Probabilidad de ocurrencia de la amenaza Casi Seguro (la más alta en PILAR) Probabilidad en valor ARO = 100 (PILAR calcula internamente la probabilidad siempre con los valores ARO independientemente de la escala que se utilice)
Impacto = Activo x Degradación= 10 x 100%= 10
Probabilidad ARO = 100
Paso 3 Evaluar si existen factores contextuales
Se valoran los factores contextuales (agravantes o atenuantes). Pueden agravar o atenuar tanto la probabilidad como la degradación del activo.
Ejemplo factor contextual aumento en un 30% la probabilidad de la amenaza.
Probabilidad ARO=100×30%= 130
Paso 4 Evaluar el riesgo potencial
En PILAR, el Riesgo Potencial, es aquel que no tiene en cuenta las salvaguardas.
Rp=Impacto x Probabilidad= 10 x 130*
El riesgo no aumenta igual al pasar de 1 a 10 eventos al año que al pasar de 100 a 110.
Para reflejar esta realidad, PILAR convierte la frecuencia de una amenaza ARO a un valor de probabilidad mediante una función logarítmica del tipo f(x) = a + b ln (x) o similar, no revelada en la documentación oficial. Este ajuste permite que la probabilidad crezca de forma más controlada y realista. Asimismo este ajuste evita valores de probabilidad iguales o cercanos a una probabilidad nula o iguales o cercanos a una probabilidad absoluta.
Por tanto con el ajuste logarítmico quedaría
Rp=Ip x Pp= 10 x 0,87 = 8,7
El resultado es un valor numérico de riesgo, limitado a un máximo de 9,9.
A modo de ejemplo para los distintos niveles de probabilidad que se pueden seleccionar en PILAR esos son los valores ARO y el valor tras el ajuste logarítmico:
| Código | Probabilidad | Ocurrencia | Frecuencia-ARO | Probabilidad-PILAR |
| CS | Casi seguro | A diario | 100 | 0,86 |
| MA | Muy alta | Mensualmente | 10 | 0,77 |
| P | Posible | Una vez al año | 1 | 0,68 |
| PP | Poco probable | Entre 2 y 5 años | 0,1 | 0,59 |
| MR | Muy rara | Cada más de 5 años | 0,01 | 0,51 |
La heurística de la probabilidad es un conjunto de atajos mentales o reglas empíricas que las personas utilizan para estimar la probabilidad de que ocurra un evento provocando que se subestimen o sobreestimen riesgos que podrían tener consecuencias significativas. Lo que pretende PILAR con este ajuste de probabilidad es que el analista de riesgos entienda que la probabilidad 0 no existe y el principio de prudencia en todo análisis de riesgos recomienda asumir que la probabilidad en el mejor de los casos debería considerarse como al menos de un 50%. De la misma forma la probabilidad del 100% tampoco existe ya que sino estaríamos en un escenario de hechos y no de riesgos. De ahí que PILAR, salvo ajustes manuales del valor de Frecuencia ARO, sólo toma valores de probabilidad entre el 51% y el 86%.
Una posible función logarítmica de ajuste de probabilidad en PILAR podría ser algo como :
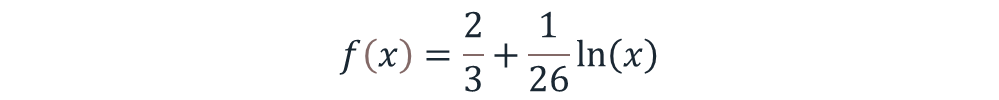
Otra posible función logarítmica de ajuste de probabilidad en PILAR que si encajaría mejor sería de la forma:
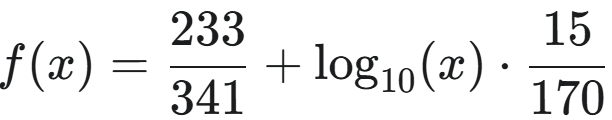
A continuación dejamos una lista no exhaustiva de ajuste de PILAR entre Frecuencia ARO y Valor de Probabilidad. Versión PILAR RM (2024,3,30 – 10,7,2024). Para que aquellos que quieran puedan usar los datos para ajustarlos a alguna función que se acerque más a la autentica que use PILAR. Cabe destacar que tomando el valor ARO más bajo que deja la aplicación 0,001 PILAR asocia una Probabilidad del 42%.
| Frecuencia-ARO | Probabilidad-PILAR |
| 0,001 | 0,42 |
| 0,01 | 0,51 |
| 0,05 | 0,57 |
| 0,1 | 0,59 |
| 0,2 | 0,62 |
| 0,3 | 0,64 |
| 0,4 | 0,65 |
| 0,5 | 0,66 |
| 0,7 | 0,67 |
| 1 | 0,68 |
| 2 | 0,71 |
| 3 | 0,73 |
| 5 | 0,74 |
| 6 | 0,75 |
| 8 | 0,76 |
| 10 | 0,77 |
| 12 | 0,78 |
| 15 | 0,79 |
| 20 | 0,8 |
| Frecuencia-ARO | Probabilidad-PILAR |
| 25 | 0,81 |
| 35 | 0,82 |
| 50 | 0,83 |
| 60 | 0,84 |
| 80 | 0,85 |
| 100 | 0,86 |
| 135 | 0,87 |
| 150 | 0,88 |
| 250 | 0,89 |
| 320 | 0,9 |
| 400 | 0,91 |
| 500 | 0,92 |
| 600 | 0,93 |
| 750 | 0,94 |
| 1000 | 0,95 |
| 1500 | 0,96 |
| 2000 | 0,97 |
| 2200 | 0,98 |
| 2622 | 0,99 |
Paso 5: Evaluar las Salvaguardas
Las salvaguardas son medidas de seguridad que mitigan el riesgo. PILAR nos permite evaluar la madurez y eficacia de cada una de ellas (basadas en marcos como el ENS o la ISO 27001) en una escala de L0 (inexistente) a L5 (optimizada). En concreto PILAR asigna los siguientes valores a la madurez de las salvaguardas L0 (0%), L1 (10%), L2 (50%), L3 (80%), L4 (90%), L5 (100%).
Por tanto si una salvaguarda tiene eficacia reduciendo la degradación del activo por la amenaza con cierta madurez, la aplicación de esa salvaguarda hará que la degradación baje.
Si la salvaguarda tiene eficacia sobre la probabilidad con cierta madurez, la aplicación de esta salvaguarda hará que la probabilidad de esa amenaza sobre el activo baje.
Una salvaguarda madura y bien gestionada será mucho más efectiva a la hora de mitigar el riesgo.
Ejemplo
Salvaguarda 1 que reduce la probabilidad de la amenaza en un 70%. Tiene una madurez de implantación L2 (50%)
Probabilidad Residual ARO = Pp x (1 – (eficacia de la salvaguarda x madurez salvaguarda))
Pr = Pp x (1 -(0.7×0.5)) = 130 x ( 1 – 0,35) = 130 x 0,65 = 84,5* => Ajuste logarítmico = 0,85
* PILAR realiza un ajuste logarítmico a la probabilidad
Salvaguarda 2 que reduce la degradación de la amenaza en la dimensión de Integridad en un 70%. Tiene una madurez de implantación L2 (50%).
Impacto Residual = Ip x (1 – (eficacia de la salvaguarda x madurez salvaguarda))
Ir = Ip x (1 – (0,7 x 0,5)) = 10 x (1 – 0.35) = 10 x 0,65 = 6,5
Paso 6: El Cálculo Final del riesgo (Impacto x Probabilidad = Riesgo)
Una vez reduciendo los valores de la probabilidad y el impacto por las distintas salvaguardas, el resultado es un valor numérico, limitado a un máximo de 9,9, que nos permite comparar, priorizar y, en definitiva, gestionar nuestros riesgos de forma objetiva y coherente.
Rr=Ir x Pr= 6,5 x 0,85 = 5,5
Lo que se pretende con este ejemplo sencillo es intentar entender el algoritmo de cálculo de PILAR.
El resultado es mucho más complejo ya que PILAR permite dependencias entre activos (tanto totales como parciales), cálculo del riesgo acumulado como repercutido, dominios de seguridad…


Comentarios recientes